set 2 challenges
9. Implement PKCS#7 padding
now i had heard of/seen PKCS#7 in the context of stuff like SSL certs, but PKCS#7 padding i had to look up. turns out it's just:
def pkcs_pad(block, length):
block_size = len(block)
padding_length = length - (block_size % length)
return block + bytes([padding_length] * padding_length)
10. Implement CBC mode
some good diagrams i found describing CBC mode:
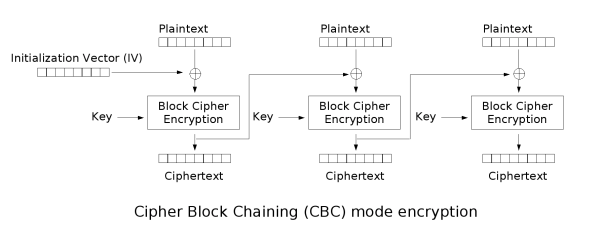
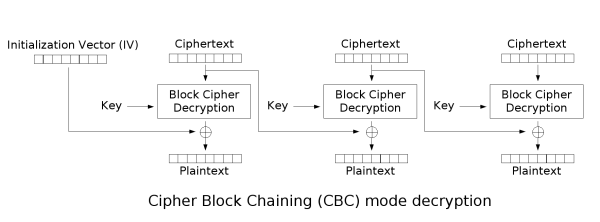
in both cases we keep a state variable which starts off containing our initialisation vector, then after each step, we store the previous cipherblock. for encryption, this state is XOR'd with the plaintext block before each encryption step. for decryption, this state is XOR'd with the plaintext after each decryption step.
something that tripped me up during implementation is that i thought for some reason the decryption steps would work in reverse on the ciphertext, i.e. the first cipher block being the last 16 bytes of the whole ciphertext. this is not the case.
(see code from set 1 for source of aes_ecb_decrypt byte_xor etc.)
def aes_ecb_encrypt(ciphertext, key):
cipher = AES.new(key, AES.MODE_ECB)
return cipher.encrypt(ciphertext)
def aes_cbc_encrypt(plaintext, key, iv):
# pad plaintext so its length is multiple of 16 bytes
# then chunk it into 16 byte blocks
blocks = list(chunk(pkcs_pad(plaintext, 16), 16))
# use initialisation vector as first previous cipherblock
prev_cipherblock = iv
result = b''
for block in blocks:
xord = byte_xor(prev_cipherblock, block)
prev_cipherblock = aes_ecb_encrypt(xord, key)
result += prev_cipherblock
return result
def aes_cbc_decrypt(ciphertext, key, iv):
blocks = list(chunk(ciphertext, 16))
prev_cipherblock = iv
result = b''
for block in blocks:
decrypted = aes_ecb_decrypt(block, key)
xord = byte_xor(prev_cipherblock, decrypted)
prev_cipherblock = block
result += xord
return result
now let's try encrypting then decrypting something with our 'manual' CBC mode functions (using a IV of all zero bytes)
s = b'the industrial revolution and its consequences have been a disaster for the human race'
key = b'YELLOW SUBMARINE'
a = aes_cbc_encrypt(s, key, bytes(16))
aes_cbc_decrypt(a, key, bytes(16))
# b'the industrial revolution and its consequences have been a disaster for the human race\n\n\n\n\n\n\n\n\n\n'
# note the padding (10 padding bytes with value of 10 (which is \n in ascii))
seems to work perfectly, let's give it a go on the encrypted data from the challenge)
with open('./data/c10.txt') as file:
s = base64.b64decode(file.read())
c = aes_cbc_decrypt(s, key, bytes(16))
print(c)
11. An ECB/CBC detection oracle
here we are asked to write a function that will generate a random key, and flip a coin to determine if we encrypt the plaintext with ECB or CBC mode. additionally we should pad both sides of the plaintext with some random bytes between 5-10 bytes long (length also chosen randomly).
we must then look at the output ciphertext and detect which mode was used.
def generate_key():
return get_rand_bytes(16)
def get_rand_bytes(bytes_):
return secrets.randbits(bytes_ * 8).to_bytes(bytes_, 'big')
def pad_with_rand(plaintext):
pad = get_rand_bytes(random.randint(5, 10))
return pad + plaintext + pad
def encryption_oracle(plaintext, use_ecb = None):
if use_ecb == None:
use_ecb = random.randint(0, 1)
padded_plaintext = pad_with_rand(plaintext)
if use_ecb:
return aes_ecb_encrypt(pkcs_pad(padded_plaintext, 16), generate_key())
else:
return aes_cbc_encrypt(padded_plaintext, generate_key(), generate_key())
recall that we can use the that fact CBC will output the same cipher blocks for any plaintext blocks which are the same. so we want to feed in some plaintext input which contains repeating blocks of bytes - let's say we want the input to be at least 4 blocks. this means we want 4 * 16 = 64 bytes. our function will pad the input with a minimum of 10 bytes (5 on each side) so we should end up with at least 64 bytes if we feed in 64 - 10 bytes. so lets go with 54 bytes of 'X'
def is_ecb(ciphertext):
blocks = list(chunk(ciphertext, 16))
return len(blocks) != len(set(blocks))
s = b'X' * 54
modes = [bool(random.randint(0,1)) for i in range(10)]
detected = [is_ecb(encryption_oracle(s, mode)) for mode in modes]
print(modes == detected)
have a play around with the number of bytes we input as the plaintext to encrypt - note how as we decrease the input length, and thus get less and less repeating blocks, it becomes more and more difficult to detect whether ECB mode was used.
12. Byte-at-a-time ECB decryption (Simple)
our task now is to (ab)use a ECB mode encryption function which uses a consistent (but unknown to us) key in order to decrypt an unknown string which will get appended to any plaintext we pass to the encrypt method.
global_key = generate_key()
unknown = base64.b64decode(b'''Um9sbGluJyBpbiBteSA1LjAKV2l0aCBteSByYWctdG9wIGRvd24gc28gbXkg
aGFpciBjYW4gYmxvdwpUaGUgZ2lybGllcyBvbiBzdGFuZGJ5IHdhdmluZyBq
dXN0IHRvIHNheSBoaQpEaWQgeW91IHN0b3A/IE5vLCBJIGp1c3QgZHJvdmUg
YnkK''')
def aes_ecb_encrypt_consistent_key(plaintext):
return aes_ecb_encrypt(pkcs_pad(plaintext + unknown, 16), global_key)
the technique outlined in this challenge is better expounded on in these articles https://yidaotus.medium.com/breaking-ecb-by-prepending-your-own-message-b7b376d5efbb https://medium.com/@hva314/breaking-the-already-broken-aes-ecb-848b358cbc7
let's figure out the cipher block size (even though we already know it - this will reveal another useful bit of info)
for i in range(20):
length = len(aes_ecb_encrypt_consistent_key(b'X'*i))
print(f'cipher length {length} | chars prepended: {i}')
cipher length 144 | chars prepended: 0
cipher length 144 | chars prepended: 1
cipher length 144 | chars prepended: 2
cipher length 144 | chars prepended: 3
cipher length 144 | chars prepended: 4
cipher length 144 | chars prepended: 5
cipher length 160 | chars prepended: 6
cipher length 160 | chars prepended: 7
cipher length 160 | chars prepended: 8
...
we can see that as we keep increasing our plaintext byte by byte, we eventually cause the input size to 'wrap' around onto the next block (one input byte + the PKCS padding). we see the cipher length increases from 144 (when we prepend nothing to the unknown string plaintext) to 160 after we prepend 6 characters. giving us a block size of 16 (which we knew). since we know it takes 6 bytes to wrap onto another block, we can also figure out the length of the unknown plaintext input.
cipher length with nothing prepended - number of bytes taken to add another block
144 - 6 = 138
here's a small toy i built to help illustrate:
legend:
- u
- the 138 byte unknown string which is appended to our plaintext input
- p
- pkcs padding
- 1
- the input we control
so we want to iterate over the range of the unknown strings length and "read" it byte by byte. we'll position the leftmost unknown byte on the last byte of a block, then we'll substitute in candidate bytes for this position (almost like we did for the XOR decryption) until we find a match
def find_next_byte(decrypted_flag):
block_size = 16
decrypted_length = len(decrypted_flag)
# will go from blocksize - 1 down to 0 as we fill up the block
# with more and more 'known' bytes
padding = b"X" * (-(decrypted_length + 1) % block_size)
target_block_idx = decrypted_length // block_size
ciphertext = aes_ecb_encrypt_consistent_key(padding)
target_block = list(chunk(ciphertext, block_size))[target_block_idx]
for i in range(256):
message = padding + decrypted_flag + bytes([i])
candidate_ciphertext = aes_ecb_encrypt_consistent_key(message)
candidate_block = list(chunk(candidate_ciphertext, block_size))[target_block_idx]
if candidate_block == target_block:
return bytes([i])
def find_flag():
decrypted_flag = b""
for i in range(138):
next_byte = find_next_byte(decrypted_flag)
decrypted_flag = decrypted_flag + next_byte
return decrypted_flag
print(find_flag())
# b"Rollin' in my 5.0\nWith my rag-top down so my hair can blow\nThe girlies on standby waving just to say hi\nDid you stop? No, I just drove by\n"
13. ECB cut-and-paste
here is my function for parsing a k=v string
def parse_query_string(s):
ret = {}
parts = s.split('&')
for part in parts:
[key, value] = part.split('=')
ret[key] = value
return ret
and here's the one for encoding a k=v string with some email input value
def profile_for(s):
s = re.sub(r'[&=]', '', s)
encoded_string = f'email={s}&uid=10&role=user'
return encoded_string
now let's write two more that "wrap" the previous with CBC mode encrypt/decrypt
def encrypted_profile_for(s):
encoded_string = profile_for(s).encode()
return aes_ecb_encrypt(pkcs_pad(encoded_string, 16), global_key)
def decrypt_profile(s):
plaintext = aes_ecb_decrypt(s, global_key)
return parse_query_string(plaintext.decode())
our goal for this challenge now is to find a way to use the resulting ciphertexts from the
encrypted_profile_for function in order to decrypt and parse some ciphertext
which will give us a user object with role:admin
let's look at what happens when we encrypt and decrypt with some example email as input
s = 'foo@bar'.com
profile_for(s)
# '[email protected]&uid=10&role=user'
profile_ciphertext = encrypted_profile_for(s)
# b'\xd5\xbd\xeb\x1966\x1e\x1ch\x00\xf3\xdbY)\xc3\xc7\x1c\x1a1G\xe9bU\xcc\xc5\xce,\x99\xd7\xe8)\x0b]XfZ]\xdb\xfao\x94\xe2k\xe2\xafdx\x1e'
profile_plaintext = decrypt_profile(encrypted_profile_for(s))
# {'email': '[email protected]', 'uid': '10', 'role': 'user\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e'}
similar to the previous challenge, we can try and adjust the input message length to line up certain points on the boundaries of blocks. since the part we want to change is luckily right at the end of the string, we can just adjust the length of the string until the bit we want to replace is on it's own on the last block. we'll then figure out a ciperblock which when decrypted reads 'admin'
we can only control the email value in the input message. to figure out what
length of bytes we need to pass in, we can take a dummy encoded profile which
has no email value, and calculate the length we need to add for message_length % 16 = len('user')
16 - (len('email=&uid=10&role=user') % 16) + len('user')
# 13
s = 'A' * 13
list(chunk(profile_for(s), 16))
# ['email=AAAAAAAAAA', 'AAA&uid=10&role=', 'user']
list(chunk(encrypted_profile_for(s), 16))
# [b'\xc9\x14-\x92y\xc0\xdf\xb5\x81\x1dd\xdd=k\xe3\xb0', b'$\xc9\x87l\xfe\x15TlqH^\xcfD\x83>i', b'_\xd8\x10\x199\x8b\x94\xb4\x1aQ\xd5J,\xb3\x15\x16']
let's replace this last cipherblock with one which contains 'admin'
ciphertext_with_admin = aes_ecb_encrypt(pkcs_pad(b'A' * 16 + b'admin', 16), global_key)
admin_block = list(chunk(ciphertext_with_admin, 16))[-1]
# b']\xb5xLv\xf0Q\xb2\xc4a\x0e\x14\xa5\x7fD\xd2'
# take all but last block and add it to admin block
cut_pasted_blocks = list(chunk(encrypted_profile_for(s), 16))[:2] + [admin_block]
ciphertext = b''.join(cut_pasted_blocks)
plaintext = aes_ecb_decrypt(ciphertext, global_key)
# b'email=AAAAAAAAAAAAA&uid=10&role=admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b'
parse_query_string(plaintext.decode())
# {'email': 'AAAAAAAAAAAAA', 'uid': '10', 'role': 'admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b'}
14. Byte-at-a-time ECB decryption (Harder)
this is fairly similar to challenge 12, except that we have the addition of some random prefix on top of the prefix we control.
let's write the function that will encrypt our plaintext with this random prefix
def get_random_prefix():
return get_rand_bytes(random.randint(0, 16))
random_prefix = get_random_prefix()
def aes_ecb_encrypt_random_prefix(plaintext):
return aes_ecb_encrypt(pkcs_pad(random_prefix + plaintext + unknown, 16), global_key)
we can pretty much reuse the exact logic from challenge 12, just making sure to make into account the length of the random prefix as part of our controlled padding prefix
def find_next_byte(decrypted_flag):
block_size = 16
decrypted_length = len(decrypted_flag)
# will go from blocksize - 1 down to 0 as we fill up the block
# with more and more 'known' bytes
padding = b"X" * (-(decrypted_length + 1 + len(random_prefix)) % block_size)
target_block_idx = (decrypted_length + len(random_prefix)) // block_size
ciphertext = aes_ecb_encrypt_random_prefix(padding)
target_block = list(chunk(ciphertext, block_size))[:target_block_idx + 1]
for i in range(256):
message = padding + decrypted_flag + bytes([i])
candidate_ciphertext = aes_ecb_encrypt_random_prefix(message)
candidate_block = list(chunk(candidate_ciphertext, block_size))[:target_block_idx + 1]
if candidate_block == target_block:
return bytes([i])
def find_flag():
decrypted_flag = b""
for i in range(138):
next_byte = find_next_byte(decrypted_flag)
decrypted_flag = decrypted_flag + next_byte
return decrypted_flag
print(find_flag())
# b"Rollin' in my 5.0\nWith my rag-top down so my hair can blow\nThe girlies on standby waving just to say hi\nDid you stop? No, I just drove by\n"
15. PKCS#7 padding validation
now we need to write a function to (validate and) strip PKCS#7 padding. recall
that in our implementation of the padding function pkcs_pad, if the string
passed in is a multiple of block size - we still append a padding (a whole
padding block i.e. b'\x10' 16 times.
by doing this we know the last byte is always a padding byte so we can
easily parse and strip padding.
def strip_pkcs_padding(s):
if type(s) != bytes:
s = bytes(s, 'utf-8')
blocks = list(chunk(s, 16))
padding_block = blocks[-1]
if len(padding_block) != 16:
raise Exception('padding invalid')
last_byte = padding_block[-1]
if last_byte not in range(1, 17):
raise Exception('padding invalid')
test_padding = last_byte.to_bytes(1, byteorder='big') * last_byte
if padding_block != test_padding:
raise Exception('padding invalid')
return b''.join(blocks[:-1])
16. CBC bitflipping attacks
i feel like this one should've been named byteflipping attack
let's first write out the two functions, then explore the logic of how to break it.
import urllib.parse
global_key = generate_key()
global_iv = generate_key()
target_substring = ';admin=true;'
def encrypt_cookie(userdata):
prepend = 'comment1=cooking%20MCs;userdata='
append = ';comment2=%20like%20a%20pound%20of%20bacon'
plaintext = prepend + urllib.parse.quote(userdata) + append
return aes_cbc_encrypt(plaintext.encode(), global_key, global_iv)
def has_admin(ciphertext):
plaintext = aes_cbc_decrypt(ciphertext, global_key, global_iv)
print(plaintext)
return target_substring.encode() in plaintext
we're tasked with trying to get some decrypted string that contains the
;admin=true; string (with unescaped ; and = chars)
for the purpose of this exercise i'll fix the key and iv to (generated with
generate_key):
global_key = b'\x15\\\xa0\xd4\x8afw\x81\xe8\x8e 3a\x04\xea\\'
global_iv = b'\xe4OO\xc4\xed\x08\x17:#""\xe7\xc7OUe'
our target string is 12 bytes long so let's input 12 'x' characters and see what the blocks look like
# plaintext blocks
[b'comment1=cooking',
b'%20MCs;userdata=',
b'xxxxxxxxxxxx;com',
b'ment2=%20like%20',
b'a%20pound%20of%2',
b'0bacon\n\n\n\n\n\n\n\n\n\n']
# ciphertext blocks
[b'\xd93\xf3\xd5u\x84B\x1d\xe8\xb5\xfc\xd2\x0fp\xc7\x9d',
b'N\x84\xa8\x8c6y\xad\xe2W\x8f\x06\x19\x9a\x92\xb4\xd3',
b"'q\xb0H\t}P\xbd+>\x06\x81\xce\xfa\r\xdb",
b'\x03\xf2\x8b\xad\x96\x91\x99D\xa3\xbd/x\xd5\x17\x0c\xaf',
b'v\xf0w\xe8\nb}>\xd9\xf2\x8c\x01\xd9[\xd0\x18',
b'\x9b\xbc\xae\xe8\xdc_\xad\xcag(\xd5:\xe6\xe8\x919']
we can see that luckily our input starts at the beginning of a block (block 3). makes things slightly simpler.
to modify the decrypted plaintext in our target substring (the 'xxxxxxxxxxxx' in block 3), we will need to modify the bytes in the same position on block 2. this is because in CBC mode, each current block gets XOR'd with the previous ciphertext block (or the IV if current block is first block) - so we know that modifying a byte on the previous block will modify a byte at the same index on the next block.
we can loop through each index of our target substring, then similar to
exercise 12, loop through every byte value until our modified decrypted block
3 substring reads ;admin=true;
s = encrypt_cookie('x' * 12)
blocks = list(chunk(s, 16))
flip_bytes = bytearray()
for idx, char in enumerate(target_substring):
target = ord(char)
for i in range(256):
candidate_byte = (i).to_bytes(1, 'big')
block_1 = bytearray(blocks[1])
block_1[idx] = i
# block_1_modified = candidate_byte + blocks[1][1:]
modified_cipher = b''.join([blocks[0], bytes(block_1)] + blocks[2:])
modified_plaintext = aes_cbc_decrypt(modified_cipher, global_key, global_iv)
chunks = list(chunk(modified_plaintext, 16))
if chunks[2][idx] == target:
flip_bytes.append(i)
break
block_1 = bytearray(blocks[1])
blocks[1] = bytes(flip_bytes) + blocks[1][len(target_substring):]
print(has_admin(b''.join(blocks)))
# b'comment1=cooking\xa8\xe0\xa4o\x94\xc5\x8b\xea @\xe9u\x0e\xcf\x1b@;admin=true;;comment2=%20like%20a%20pound%20of%20bacon\n\n\n\n\n\n\n\n\n\n'
# True
